ArduinoでSTEM教育​ 実践編：ライントレースカーをPID制御する

前回作成したライントレースカーはガタガタ走行でした。今回は、自動制御でよく用いられるPID制御で、ラインに対して滑らかな走行ができるようにプログラムします。難しそうに感じるかもしれませんが、実際にモノを作ってみると理解度が断然上がります。

使用する部品一覧

使用する車は、前回の記事(ArduinoでSTEM教育​ 実践編：ライントレースカー)で作成したものを使用します。 電子部品の説明、回路図、ブレッドボード図はこちらを参照してください。

PID制御とは

前回作成したライントレースカーは、左右のフォトリフレクタがラインを検出する/しないの２値で、車の進行方向を制御していました。単純な制御なので理解しやすいですが、車はガタガタ走行になってしまいます。滑らかに走行するためには、フォトリフレクタのライン検出をアナログ値で取得して、 車の進行方向を 細かく調整してあげれば良いのです。その手法というのが、PID制御です。

PID制御は、出力値が目標値に近づくように、入力値を制御する、フィードバック制御の一種です。PIDは、「Proportional-Integral-Differential」を略した表記です。 Proportional は比例、Integralは積分、Differentialは微分を意味します。 これを式で表すと、下記のとおりとなります。 ライントレースカーでは、出力値は左右のフォトリフレクタの検出値、目標値は左右のフォトリフレクタがラインを検出しない値、入力値は左右のタイヤ（モータ）の回転速度です。

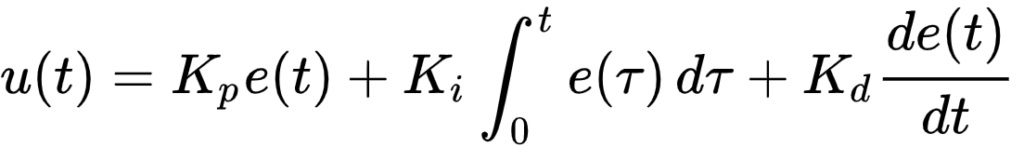
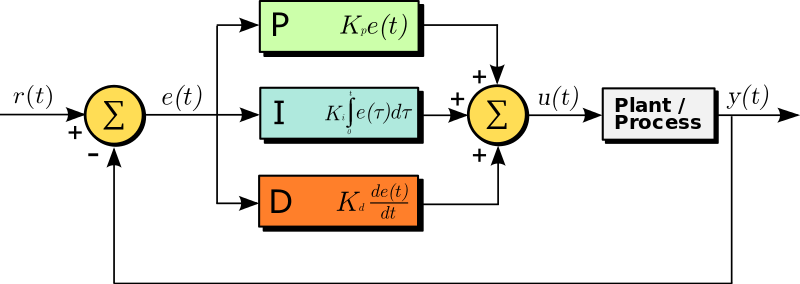
P制御

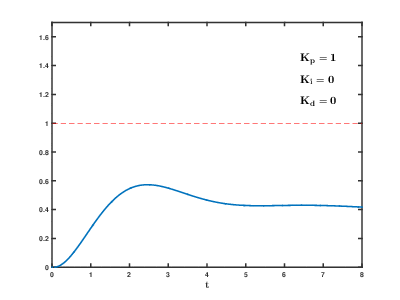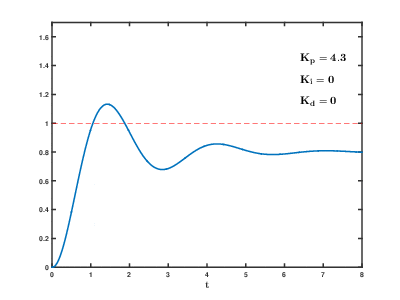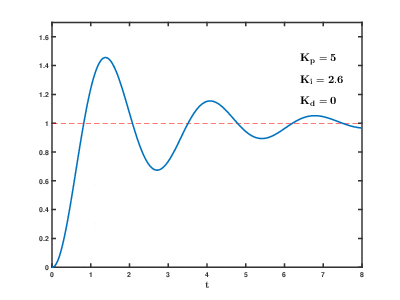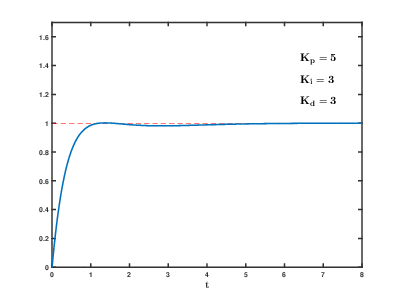
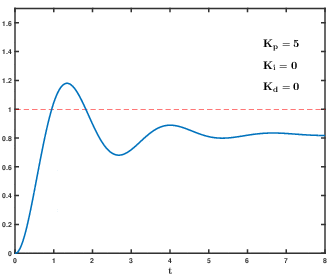
P制御（比例制御）は、ある時における操作量（タイヤの回転速度）を出力値（フォトリフレクタ検出値）と目標値（フォトリフレクタのライン未検出値）の差分の１次関数として制御します。すなわち、ラインから大きくハズレている場合は、左右のタイヤ回転速度差を大きくして、素早くラインに戻ります。ラインから少ししか外れていない場合は、 左右のタイヤ回転速度差を 小さくして、徐々にラインに戻ります。しかし、P制御には弱点が２つあります。

１つ目の弱点は、オフセットです。差分を操作量とするため、目標値近辺では操作量が非常に小さくなり、目標値から少しずれたところで安定してしまいます。これをオフセットまたは定常偏差と呼びます。

２つ目の弱点は、オーバーシュートです。目標値から大きくハズレているときは操作量が大きいので、目標値に到達してもすぐには反応できず、大きく通り過ぎてしまいます。これをオーバーシュートと呼びます。

I制御

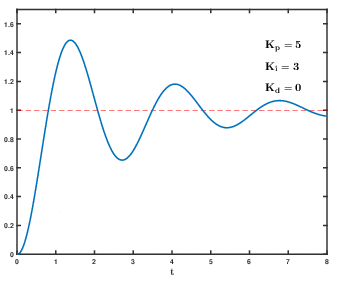
I制御（積分制御）は、P制御の弱点であるオフセットを補います。直線を走っている状態であれば、P制御だけでも安定して走ることができます。しかし、カーブでは、オフセットによってカーブの外側で安定しようとします。そのため、曲がれきれずにコースアウトし易くなります。これを改善するために、 過去から現在までの偏差の累積をもとに制御します。 もう少し具体的に説明すると、小さなオフセットで安定していたとしても、そのオフセットを10ms毎に積み重ねていくと、100ms後には10倍の値になります。この値に応じてタイヤの回転速度を制御します。

D制御​​

D制御（微分制御）は、P制御の弱点であるオーバーシュートを補います。直線から急カーブに突入すると、素早く対応できずにコースアウトしてしまいます。これに対応するためには、「過去の偏差」と「現在の偏差」の差分に応じて制御します。 PI制で 直線で安定走行している場合の偏差はゼロですが、カーブに突入すると偏差が急に大きくなります。カーブが急であればあるほど大きくなります。

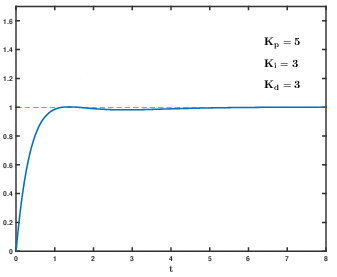
限界感度法によるPIDパラメータ調整

PIDの各パラメータ（Kp, Ki, Kd）は、シミュレーションを基に実物を動作させながら合わせ込むのが一般的です。とはいえ、全てのパラメータをランダムに調整していては、とてつもなく時間がかかってしまう。そこで、パラメータ調整の経験則として知られている「限界感度法」を用います。限界限度法の手順を以下に示します。

最初はP制御だけで調整します。Kpを０から少しずつ大きくしていき、制御量が安定して、それ以上大きくすると振動が発散してコースアウトする手前の状態を求めます。このときのKpを限界感度と呼び、Kuで表します。また、その時の制御量の振動周期をPuとします。これらの値は、シリアルプロッタでグラフを見ながら調整すると良いと思います。

次に、KpとKdを求めるために、 積分ゲインをKi = Kp / Ti、 微分ゲインをKd = Kp * Tdとして、最初のPID制御式に代入すると、下記のとおりになります。

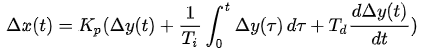
さらに、伝達関数で表現すると、下記の式になります。

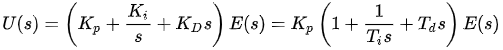
TiとTdは、限界限度法の経験則から下表のように算出できます。

制御の種類	Kp	Ti	Td
P	0.50Ku	–	–
PI	0.45Ku	0.83Pu	–
PID	0.60Ku	0.50Pu	0.125Pu

例えば、Ku=0.5, Pu=0.8secだった場合、PID制御パラメータは以下のように計算できます。
Kp = 0.60Ku = 0.6*0.5 = 0.3
Ki = Kp/Ti = 0.3/(0.50*0.8) = 0.75
Kd = Kp*Td = 0.3*(0.125*0.8) = 0.03

プログラム

I制御やD制御をするためには、フォトリフレクタの過去の検出値を保持しておく必要があります。フォトリフレクタは左右に２個あるため、それぞれ個別に保持しなければならないので、PIDクラスを作成します。

//www.stemship.com
//2019.11.22
class PID {
  private:
    int _diff[2];
    float _integral;
    int _deltaT;
    float _p, _i, _d, _pid;
    
  public:
    //コンストラクタ
    PID (int deltaT) {
      _deltaT = deltaT;
    }
    
    //PID値を返す
    int getPID(int now, int target, float KP, float KI, float KD) {
      _diff[0] = _diff[1];
      _diff[1] = now - target;
      _integral += (_diff[0] + _diff[1]) * _deltaT;

      _p = KP * _diff[1];
      _i = KI * _integral;
      _d = KD * (_diff[1] - _diff[0]) / _deltaT;
      _pid = _p + _i + _d;
      _pid = constrain(_pid, -255, 255);
      return _pid;
    }
    int getP() {
      return _p;
    }
    int getI() {
      return _i;
    }
    int getD() {
      return _d;
    }
}

メインプログラムは、前回の記事(ArduinoでSTEM教育​ 実践編：ライントレースカー) をベースにPID制御を組み込んでいます。３行目～６行目のパラメータは、各々の環境で調整して決めてください。フォトリフレクタの目標値は「 const int valTarget = 940 」で設定しています。これはラインの無い床を検出した場合の値になります。PID制御では真ん中のセンサを使用しないため、プログラムから削除しても構いませんが、デバッグ用途で利用できるかもしれないため残しています。

//www.stemship.com
//2019.11.22
#include "Motor.h"
#include "PID.h"
#define DELTA_T 50 //ループ時間[ms]
#define KP 0 //各々の環境で調整して決める
#define KI 0 //各々の環境で調整して決める
#define KD 0 //各々の環境で調整して決める

//右と左のモータ
Motor motorR = Motor(11, 10);
Motor motorL = Motor(6, 5);

//PID制御
PID pidR = PID(DELTA_T);
PID pidL = PID(DELTA_T);
const int valTarget = 940;

//トラッキング用センサのピン番号(Analog Input)
const int pinSensorR = 1; //右側 
const int pinSensorL = 5; //左側 
const int pinSensorC = 3; //真ん中 

//車の速度
const int carSpeed = 128;

//車の動作関数
void runForward();
void runRight();
void runLeft();
void runBack();

void setup() {
  // put your setup code here, to run once:
  pinMode(pinSensorR, INPUT);
  pinMode(pinSensorL, INPUT);
  pinMode(pinSensorC, INPUT);

  //シリアル通信
  Serial.begin(9600);
}

void loop() {
  unsigned long now = millis();
  int valSensorR = analogRead(pinSensorR);
  int valSensorL = analogRead(pinSensorL);
  int valSensorC = analogRead(pinSensorC);
  int pidValR = pidR.getPID(valSensorR, valTarget, KP, KI, KD);
  int pidValL = pidL.getPID(valSensorL, valTarget, KP, KI, KD);
 
  Serial.print(valSensorR);
  Serial.print(",");
  Serial.print(valSensorL);
  Serial.print(",");
  Serial.print(valSensorC);
  Serial.print(",");
  Serial.print(pidValR);
  Serial.print(",");
  Serial.print(pidValL);
  Serial.print(",");
  Serial.print(pidR.getP());
  Serial.print(",");
  Serial.print(pidR.getI());
  Serial.print(",");
  Serial.print(pidR.getD());
  Serial.print("\n");
  
  motorR.forward(constrain(carSpeed + pidValR - pidValL, 0, 255));
  motorL.forward(constrain(carSpeed + pidValL - pidValR, 0, 255));

  //ループ時間[ms]
  delay(DELTA_T);
}

//WAITに移行するとき
void enterWaiting() {
  motorR.stop(false);
  motorL.stop(false);
}

//RUNに移行するとき
void enterRunning() {
  motorR.forward(255);
  motorL.forward(255);
}

//前進
void runForward(int val) {
  motorR.forward(val);
  motorL.forward(val);  
}

//後退
void runBack(int val) {
  motorR.reverse(val);
  motorL.reverse(val);
}

//右旋回
void runRight(int val) {
  motorR.stop(false);
  motorL.forward(val);
}

//左旋回
void runLeft(int val) {
  motorR.forward(val);
  motorL.stop(false);
}

＜参考にしたサイト＞
・ https://ja.wikipedia.org/wiki/PID%E5%88%B6%E5%BE%A1
・ https://monoist.atmarkit.co.jp/mn/articles/1007/26/news083.html